avl-tree-pic-1
Go up to the Labs table of contents page
A binary tree is a tree with a maximum of two children per node. Tree traversals are commonly associated with binary trees. A pre-order traversal processes the given node first and then processes its left and then right subtrees. In an in-order traversal, first the node's left subtree is processed, followed by the node itself, and finally its right subtree. A post-order traversal operates on the left subtree, followed by the right subtree, and finally on the node itself.
A binary search tree is a binary tree that imposes an ordering on its nodes. A node's left child has a lesser value, while its right child has a greater value. Binary search trees are useful for efficient insertion, deletion, and lookup of items with a certain key. As we'll see in this lab, variations of binary search trees offer different performance characteristics.
The Wikipedia article on Expression trees, especially the section on construction of expression trees. Also the 05: Trees slide set.
Makefile-pizza - not Makefile-pizza.txt, not Makefile-Pizza, not Makefilepizza. If it is not named correctly, it will not work with our grading scripts, and you will not get credit for that part of the lab.For this lab you will be using a stack to help you read in a postfix expression into an expression tree. While this is similar to lab 3, you will instead be ultimately creating a expression tree for the postfix expression, rather than evaluating it and leaving the result on the stack. You should use the STL stack class for this lab.
Your tree calculator should read in expressions in postfix notation -- you can assume that these will be well-formed expressions as we did in lab 3. You will need to build an expression tree using the algorithm described in the Wikipedia article on Expression trees, specifically the section on construction of expression trees. Trees similar to this type of expression tree are used extensively in compilers.
You must use the skeleton source files provided here as a basis for your prelab. The following guidelines apply to your implementation:
readInput() method. Points will be deducted if you do so.printOutput() method is to add calls to your implemented printPrefix(), printPostfix(), and printInorder() methodsNote that the code will not compile out of the box -- you need to add code so that the printOutput() method in TreeCalc works.
You should only submit the following five files:
Note that the last three files should not be modified at all! If you have additional code to include, put it in TreeCalc.cpp or TreeCalc.h (you should not need to use additional classes). Just in case it wasn't clear yet, all your modifications should be in the TreeCalc.h and TreeCalc.cpp files.
Your fully functional tree calculator code should do the following:
Make sure your destructor works! We will be testing that to see if there are any memory leaks.
A few notes:
atoi. To use atoi, you must include #include <cstdlib>. Without that #include, it may work on your machine, but it will not work on the grading server.printOutput() -- this is the one change you can make to this method)Postfix notation (also known as reverse Polish notation) involves writing the operators after the operands. Note how parentheses are unnecessary in prefix or postfix notation. Your print methods must print in the following format. The only spaces are on either side of the operators. Your entire expression must be printed on a single line that terminates with a newline character. You should put parenthesis around each infix operation, regardless if it is needed according to operator precedence.
((34 + 6) - (-8 / 4))34 6 + -8 4 / -- + 34 6 / -8 4Below is a sample execution run to show you the input and output format we are looking for.
Enter elements one by one in postfix notation
Any non-numeric or non-operator character, e.g. #, will terminate input
Enter first element: 34
Enter next element: 6
Enter next element: +
Enter next element: -8
Enter next element: 4
Enter next element: /
Enter next element: -
Enter next element: #
Expression tree in postfix expression: 34 6 + -8 4 / -
Expression tree in infix expression: ((34 + 6) - (-8 / 4))
Expression tree in prefix expression: - + 34 6 / -8 4
The result of the expression tree is 42 For this in-lab, you will implement a Binary search tree. The required class declarations are located in BinaryNode.h and BinarySearchTree.h. You may want to create private helper methods for BinarySearchTree, as done for the implementation of remove, which is already provided for you. Notice how the private methods take a BinaryNode as a parameter. This allows them to recur over a subtree, a common implementation technique.
Do NOT alter BSTPathTest.cpp. This program will be used to run automated tests on your implementation. Do not change it.
The test program reads a sequence of a sequence of instruction/word pairs and attempts to operate on your tree. Example test files are located in the inlab directory. - Insert I <word> - Remove R <word> - Lookup L <word>
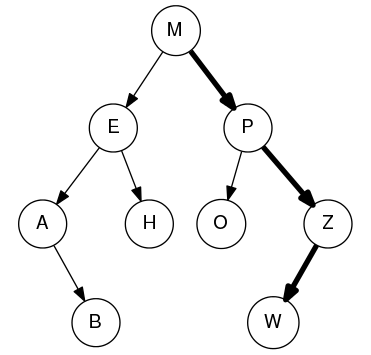
The Lookup instruction will call the pathTo() method defined on your tree. pathTo() must return a string representing the nodes encountered when finding an element. For instance in the following image, the bold lines indicate the path taken for locating element W.

avl-tree-pic-1
pathTo("W") would then return the string "M P Z W". Calling pathTo() on an element that doesn't exist would result in an empty string "".
To recap, submit the following files: - BSTPathTest.cpp: Do NOT modify, contains main(). - BinaryNode.h, BinarySearchTree.h: class declarations the test program requires. - BinaryNode.cpp: contains the implementation of BinaryNode. - BinarySearchTree.cpp: contains the implemention of BinarySearchTree. - Any other .cpp files required to make your program compile. - Makefile: compiles your program and produces the a.out executable.
The objective of this post-lab is to understand the runtime characteristics and trade-offs between normal Binary search trees and AVL trees. You will have to implement an AVL tree and write a brief report to compare its performance with the Binary search tree implemented for the in-lab.
The required class declarations are located in AVLNode.h and AVLTree.h. Much of the behavior of the AVL implementation is similar to that of the Binary search tree, aside from rotations and rebalancing. You may want to create private helper methods for AVLTree, as done for the implementation of remove, which is already provided for you.
Do NOT alter AVLPathTest.cpp. This program will be used to run automated tests on your implementation. Do not change it. The example test files are located in the postlab directory.
To recap, submit the following files: - AVLPathTest.cpp: Do NOT modify, contains main(). - AVLNode.h, AVLTree.h: class declarations the test program requires. - AVLNode.cpp: contains the implementation of AVLNode. - AVLTree.cpp: contains the implemention of AVLTree. - Any other .cpp files required to make your program compile. - Makefile: compiles your program and produces the a.out executable. - analysis.pdf: The report for this lab.
The report for this lab should contain the following:
We are looking for a full page (double-spaced) for parts 3 and 4 combined. You can single-space as long as it has the same length (in terms of words).