Airline Routes

Flowcharts

Pre-requisite Diagrams

Representation: Adjacency Matrix

\( A[u][v] = \left\{ \begin{array}{l l} weight & \quad \text{if ($u$,$v$) $\in$ $E$}\\ 0 & \quad \text{if ($u$,$v$) $\notin$ $E$}\\ \end{array} \right. \)

1 2 3 4 1 2 3 4

Representation: Adjacency List

Topological Sort

One valid topological sort is: v1, v6, v8, v3, v2, v7, v4, v5

This is already topologically sorted!

Another Topological Sort Example

Shortest Path Algorithms

• This version is called the "single-source" shortest path
• Given a graph \( G = (V, E) \) and a single distinguished vertex s, find the shortest weighted path from s to every other vertex in G

The weighted path length of \( v_1, v_2, \ldots , v_n \):

\( \sum_{i=1}^{n-1}c_{i,i+1} \) where \( c_{i,i+1} \) is the cost of edge \( (v_i,v_{i+1}) \)

Unweighted Shortest Path

• Special case of the weighted problem: all weights are 1
• Solution: breadth-first search; similar to level-order traversal for trees

Dijkstra's Algorithm

V Known? Dist Path v0 v1 v2 v3 v4 v5 v6

Another Dijkstra's Algorithm Example

V Known? Dist Path v1 v2 v3 v4 v5 v6

This is the same graph as in the Wikipedia article on Dijkstra's algorithm

Shortest Path Example Problem

From the ICPC Mid-Atlantic Regionals, 2009

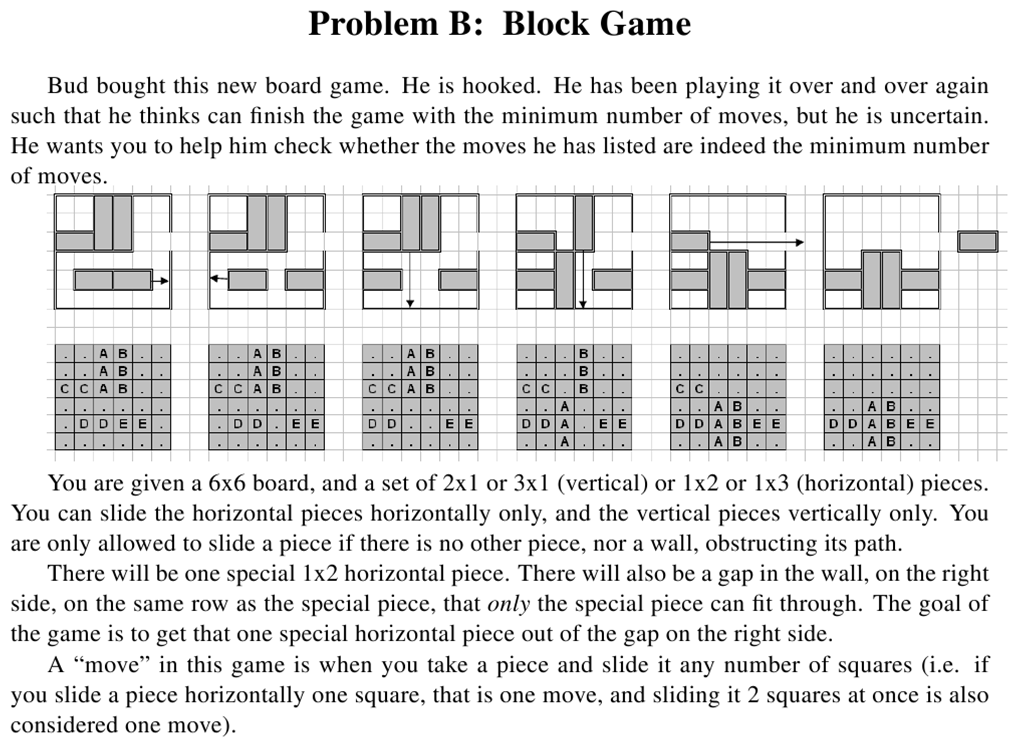
How would you drive to Seattle?

And what constitutes a "highway"?

The Eisenhower Interstate System

A Google Maps Screenshot

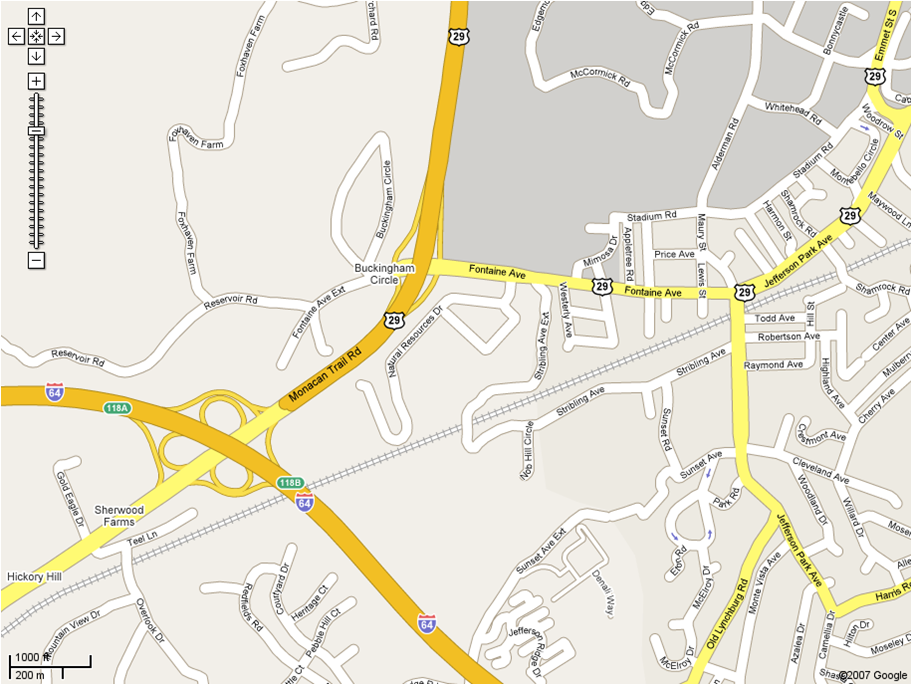
Hard

Really Hard

Spanning Trees

Original graph:

Possible spanning trees:

Minimum Spanning Trees

• Given a connected and undirected graph G = (V,E), find a graph G' = (V,E') such that:
  • E' is a subset of E
  • |E'| = |V| - 1
  • G' is connected
  • \( \sum_{(u,v) \in E'} c_{uv} \) is minimal
• G' is then a minimal spanning tree
• Applications: wiring a house, cable TV lines, power grids, Internet connections

Prim's MST Algorithm

Edges: (v1,v2), (v1,v4), (v3,v4), (v4,v7), (v5,v7), (v6,v7)

Kruskal's MST Algorithm

Edges: (v1,v2), (v1,v4), (v3,v4), (v4,v7), (v5,v7), (v6,v7)