Go up to the Labs table of contents page
In lecture we discussed Huffman coding and the construction of prefix code trees. We have also covered a variety of data structures this semester: lists, trees, hash tables, and heaps. Several of these may be useful for this lab. In addition, in this lab you are required to think about the underlying representation and efficiency of these structures.
make)make)The basic steps in compression (for the pre-lab) are:
We are also writing additional information to the file (compression ratio and tree cost), as described herein.
The basic steps in decompression (for the in-lab) are:
Huffman compression and decompression are both covered in the Heaps and Huffman slide set.
Assume that only printable ASCII characters will occur in the source (original, uncompressed) text file. That is, your program should ignore newlines and tabs, but should not ignore spaces -- thus, spaces need to be encoded, just like with other (printable) characters (note, however, that spaces are encoded differently; see the input format for details). Your program should be case-sensitive (count upper-case and lower-case versions of the same letter as different characters). The lecture notes describe which characters are to be encoded.
You must use a heap (priority queue) data structure to receive full credit on this pre-lab. You may use heap code from the slides (give said credit if you do so), or you may implement your own. You may NOT use the priority_queue class from the STL, but you may use other classes from the STL (i.e. non-heap related classes).
Real Huffman encoding involves writing bit codes to the compressed file. To simplify things in your implementation, you will only be reading and writing whole ASCII characters the entire time. To represent the zeroes and ones of the bit codes you will write the characters 0 and 1 to your output file. Yes, this means that the actual size of our compressed file will be larger than our original file (terrific, you "compressed" the charactert into the five characters 01011), but it will simplify the lab considerably.
Implementation. You will need to select several different data structures to implement Huffman compression and decompression. Don't get more complicated than is necessary, but do keep efficiency in mind. Consider the following questions:
Use the answers to these questions to guide your selection. Your solution will be judged slightly on how efficient it is (both in terms of time and space). Very inefficient solutions will lose a few points. Be sure you have a good explanation for your implementation choices:
Whatever your implementation, you should be able to accurately describe its worst case Big-Theta performance both in running time and space (memory) usage.
Serializing Data Structures. One thing we have not dealt with in previous labs is serializing various data structures (writing them to a file or standard output, and reading them back in). You will need to do this with your prefix code tree. The fact that you must read this data structure from a file and write to standard output may affect how you choose to represent it in your program. Keep in mind that the format for how to write it to a file is fixed, as described below (in the pre-lab section). You will need to re-create your Huffman coding tree from the first part of the file format described below.
operator<(): If you are creating a HuffmanNode (or similar) with an operator<() method, make sure that method is const (both in the .h file and in the .cpp file).
For the pre-lab, you will implement the Huffman encoding algorithm using a binary heap. In particular, you will need to implement all of the basic compression steps described later in this document. You may use and modify code from the lecture notes, any code you generated, but you may NOT use the STL heap class (called priority_queue) -- you can use other (non-heap related) classes from the STL.
Your program must take in a single command-line parameter, which is the name of the file whose contents will be encoded. We have some sample plain text and encoded text files (in the labs/lab10/examples/ directory) -- a description of these files is in the in-lab section. Keep in mind that, as described below, your program will need to ignore newlines and non-printable characters in the input file.
Your program should output to the standard output (i.e. cout) the exact file format described below, and nothing else. It should NOT output to a file!
As part of the file format described below, your program will need to print out the compression ratio and the Huffman tree cost. The compression ratio is defined, in bits, as: (size of the original file)/(size of compressed file). You should exclude the size of the prefix code tree in the compression ratio, and assume that the 0's and 1's you generated for the compressed file count as one bit each (rather than an 8-bit character). The Huffman tree cost is the same as described in lecture.
Your program should be in at least three files: heap.h, heap.cpp, and huffmanenc.cpp; it may contain more, depending on your implementation. The heap.h and heap.cpp will contain the heap implementation, and the huffmanenc.cpp will contain the main() method and the other Huffman encoding methods needed by your program. We'll be calling make to compile your program, so make sure your Makefile works as well.
To read in the input file character by character, see the fileio.cpp (src) file.
In an effort to both ease the in-lab implementation (as we can thus provide examples) as well as ease the grading, there is a very strict file format for a Huffman encoded message for this lab. This allows the two parts to be developed, implemented, and tested separately. Although real Huffman encoding uses bits, we will write these bits to a file using the characters 0 and 1, as that will make it easier to check and debug our code. The challenging part of reading in a file (which is done during the in-lab) is re-creating the Huffman coding tree. This is discussed in detail in the in-lab section.
The file format is as follows. There are three sections to an encoded file, each separated by a specific separator.
The first section of the file are the ASCII characters that are encoded, followed by their bit encoding. Only one such encoding per line, with no blank lines allowed. The format for a line is the ASCII character, a single space, and then the 1 and 0 characters that are the encoding for that character, followed by a newline. The order of the characters does not matter. However, your code to read in the file must be able to handle the characters in any order. If the character being written is the space character itself, you should write space instead of " "; thus a line for the space character might look like: space 101010. Keep in mind that the first character on this type of line cannot be a newline, tab, or a non-printable character. No line in this part can be more than 256 characters. You can safely assume that the data provided will be a valid Huffman coding tree (i.e. there won't be an internal node with one child, etc.).
Following that is a separator line, and is a single line containing 40 dashes and no spaces.
The second section is the encoded message, using the characters 0 and 1. You may separate these any way you would like using whitespace (space, tab, return) -- thus, you can have one per line, if you would like. The only valid characters in this section, therefore, are the two digits (0 and 1), as well as the three whitespace characters (space, tab, and newline). For the pre-lab, separating the encodings by spaces or newlines will make checking and debugging your code easier: having a space between each encoded letter, and a return between each encoded word, will help considerably. However, when the file is read in, your code MUST be able to read in a Huffman encoded message regardless of the whitespace formatting.
The next line is a separator, and is also a single line containing 40 dashes and no spaces.
The last section of the file are English text, which displays the compression ratio and the cost of the Huffman tree. This does not need to be read in by the decompression routines. As long as you output the required information, and it is easily understandable by a human, it can be in a format similar to (but not necessarily the same as) what is shown below. You can have additional information as well, as long as we can easily find what we are looking for (compression ratio and Huffamn tree cost).
For the in-lab, you can assume that we will not provide you with invalid Huffman file formats. You can safely assume that we will provide you with a few different valid file formats (a few such examples are available in the labs/lab10/examples/ directory).
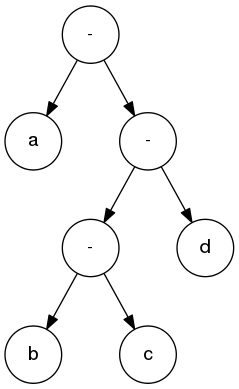
The following is the Huffman file format for example in the slide set that has the characers 'a', 'b', 'c', and 'd'.
a 0
b 100
c 101
d 11
----------------------------------------
11 100 0 101 0 0 11
----------------------------------------
There are a total of 7 symbols that are encoded.
There are 4 distinct symbols used.
There were 56 bits in the original file.
There were 13 bits in the compressed file.
This gives a compression ratio of 4.30769.
The cost of the Huffman tree is 1.85714 bits per character.The Huffman tree that this forms is the same as the one shown in the slide set (specifically, here), and is dupliated below.

Below is an equivalent version of the same file. Note that the characters are not in the same order in the previous example, the whitespace for the middle part is quite different, the English explanation in the third part says the same thing but in a different format, and the particular prefix codes are different (but note that the lengths are the same). Your in-lab code will need to be able to read in both of these files (as well as others in the labs/lab10/examples/ directory). For writing your pre-lab, you should consider having a space or a newline between the Huffman encoded characters, as that will make your code easier to check and debug.
d 11
c 101
b 100
a 0
----------------------------------------
11
100
0 1 0 1 0 0 1 1
----------------------------------------
Compression ratio: 4.31
The Huffman tree cost: 1.85 bits per characterNote that your encoding does not have to exactly match -- in particular, the bits that your program uses to encode it will depend on the implementation of your heap. So while your bits can be off, the number of bits for each character should NOT be different than the examples given.
To read in the input file character by character, see the fileio.cpp (src) file.
A few hints from experience with this in previous semesters.
operator=(), etc. Stay with the pointers, as it will save you time in the long run.Make sure your pre-lab code can read in any printable ASCII character, including spaces (which are encoded differently!), but not newlines or tabs. If you look at the ASCII table in the Huffman coding lecture notes, you want to be able to handle all of the characters in the red box. Keep in mind that text files will always have a newline character (\n) at the end of each line. Some text files might also have the carriage return character (\r) at the end of each line as well. This is from the difference in text file formats between Windows and Unix.
Your program should output to the standard output (i.e. cout) the exact file format described above, and nothing else.
There are additional examples of encodings in the labs/lab10/examples/ directory. Keep in mind that the bits that your code generates for a given character do not have to match the bits that are shown in the examples (as this will depend on the implementation of your heap), but the number of bits per character DOES have to match.
We provide a number of sample files for you to test your code with. A brief description of each is described here. The "normal" files are the English input. The "encoded" files are the Huffman encoded files, following the file format described above. Except where indicated, the middle part of each encoded file (the digits 0 and 1) has a space is inserted between each letter from the original file, so that you can see which letter is encoded as which bitcode.
dbacaad). The Huffman tree can be viewed here.0s and 1s.During in-lab, you will implement the decompression steps for the Huffman encoding. These steps are listed at the beginning of this lab document.
First, make sure that your code can read in the file -- you can download the inlab-skeleton.cpp file, which can properly read in the encoded input files.
Next, focus on creating the Huffman coding tree. There are a number of ways to go about doing this -- we present one such algorithm here. As you are (recursively) creating each node in the tree, you know the bitcode code so far to get to that node (remember that following a left child pointer generates a 0, and following a right child pointer generates a 1). We'll call this bitcode-so-far the "prefix" (as it is the prefix for all bitcodes below this node). If that prefix is one of the listed bitcodes in the first part of the file, then we are at a leaf (remember that all characters in a Huffman tree are leaves), and the node will not have any children. Otherwise, we are dealing with an internal node -- and you will have to create left and right child nodes, calling yourself recursively on each one. Keep in mind that when you call yourself recursively on the left child, you have to add 0 to the end of the prefix; likewise, you have to add 1 to the prefix for the right child. This algorithm will require you to search through the bit codes that were read in from the first part of the file. Also keep in mind that the size of the input here (the number of characters) is very small (only 80 or so) -- which means that if you choose a linear time complexity data structure (vector, for example), your code will run just fine.
Not creating a Huffman tree from the file will result in zero credit for the in-lab. The whole point of this part is to create the tree!
Lastly, read in the second part of the file, transverse your Huffman tree, and output a character when you reach a leaf node. You can output as much text as you would like, such as status updates as to how the program is progressing. The only caveat is that the decoded file must be the last thing printed, and it must be clear where the other text ends and the decoded message that you are decoding begins (a separator of dashes would be fine for this). Of course, you are more than welcome to just print out the decoded message and nothing else.
If you cannot get the Huffman decoder working during the in-lab time, then you should request a lab extension, and submit what you have done so far.
As with the pre-lab, you should ensure that those files compile successfully with make.
There are two parts to this post-lab: the time and space complexity analysis, and submitting all your (working) code again.
For the post-lab, we want you to do a time and space complexity analysis of your compression and decompression code. You'll submit a written report that describes your implementation choices, and also documents your analysis of time and space complexity. See below for a discussion about the space/time complexity.
The deliverable for the post-lab is a PDF document named postlab10.pdf. It must be in PDF format! See How to convert a file to PDF for details.
A written post-lab report (a page is fine) that includes the following. You can double-space your report, but no funky stuff with the formatting (standard size fonts, standard margins, etc.). And if you double-space your report, you need to increase the number of pages appropriately.
Worst case running time -- for this be sure to include all steps of the compression and decompression. You can leave off the cost of calculating the compression ratio, printing the cost of the tree, and printing a listing of the bit code for each character that was asked for in the pre-lab. Refer to the list of steps given earlier in the lab.
Space complexity -- for this, you should calculate the number of bytes that are used by each data structure in your implementation. The easiest way to do this is to step through your code, just as you have done for the worst case running time, and make a note each time you use a new data structure. You do not need to take into account scalar variables (loop counters, other singleton variables), focus on the data structures whose size depends on values such as the total number of characters and the total number of unique characters, and use those values in your answer.
For the post-lab, the purpose is to clean up your code from the pre-lab and in-lab, and submit all of it together. If your pre-lab and in-lab code work properly, then there is no futher clean-up to do; however, you must still submit the files along with a new Makefile.
When we run make, the code should be compiled into two executables: encoder and decoder, which are the pre-lab and in-lab code bases, respectively. Unlike the pre-lab and in-lab, you should NOT name your executables a.out! After compiling your code with make, we will test it as such:
./encoder testfile.txt > encoded.txt
./decoder encoded.txt > output.txt
diff testfile.txt output.txtThis encodes a sample text file, then decodes it. Both the original file (testfile.txt) and the final file (output.txt) should be the same, which is what the diff command does. Note that, if there are no differences between the two files, then diff does not print any output.